【Hello！とうけい】Vol.288 ガチャが外れる確率は？　ネイピア数eを用いた確率計算

　令和7年5月28日掲載

　みなさんがゲーム、特にカードゲームやボードゲームを遊ぶ際、確率を考えない事は無いでしょう。勝つか負けるか、どれだけ勝てそうかを考えるときには、必ず確率を計算して行動を決めていると思います。
　しかし、そういった身近なものでありながら、確率については何となくでとらえてしまっていることが多いものです。特に、ネイピア数eと呼ばれる数と、確率の計算との間に密接な関係がある事はあまり知られていないと思います。
　今回は、当たる確率が低いガチャを回した場合の当たりが出る確率を計算し、ネイピア数eとのかかわりも合わせて紹介したいと思います。

　コインの表が当たりの時、２回投げて当たりが出ない確率は、２回とも裏が出る確率ですから、２分の１を２回かけ合わせて４分の１です。当たる確率が２分の１といっても、２回投げれば必ず当たるわけでは無いのが重要です。
　ではサイコロで１の目が当たりの時、６回振って当たりが出ない確率はどうなるでしょうか。
サイコロを振って１が出る確率は６分の１なので、一度振って当たりが出ない確率は６分の５です。６回振って当たりが出ない確率は、６分の５を６回かけ合わせて４６６５６分の１５６２５です。計算すると0.335ぐらい、３分の１ほどは当たりが出ないことになります。
　それでは、ここに常に１％の確率で当たりが出るガチャがあるとします。このガチャで当たりを出すには何回回せば良いでしょうか。なお、当たる回数は考えず、当たりが出るか出ないかで考えます。直感的には１００回回せば１回くらいは当たりが出そうな気がします。しかし、当たり確率１％のガチャを１００回回しても当たりが出る確率は１００％にはなりません。
　当たりが出る確率を計算するにはどうすれば良いでしょうか。ガチャを１回回して外れる確率は１から当たる確率の１％を引いて９９％、つまり１００分の９９です。１００分の９９を１００回かけ合わせればガチャを１００回回した時に全て外れる確率が出せますから、それを１から引けば当たりが出る確率がわかります。しかし、１００回もかけ合わせるのは大変です。簡単に大体の確率がわかる方法は無いでしょうか。

               

　こうした計算に便利な数として、ネイピア数と呼ばれる数があります。アルファベットのeと表記するこの数は2.7くらいになるのですが、実はe分の１、つまり大体2.7分の１、計算すると３７％くらいというのが、当たる確率の分だけガチャを回した時に当たりが出ない確率の上限になります。当たる確率が低いガチャをその確率の分だけ回した時に当たりが出ない確率は、元々の当たる確率が低いほど増えていきますが、その確率は３７％を超えることはありません。
　６分の１を６回振った時に当たりが出ない確率が３４％くらいだったので、１００分の１を１００回回した時の当たりが出ない確率は３４％と３７％の間になります。実際に計算すると大体３６．６％になります。５０分の１を５０回回した場合は３６．４％くらい、２５分の１を２５回だと３６．０％程です。つまり、当たる確率が２～３％以下であれば、その確率の分ガチャを回した時の当たりが出ない確率は、大体３６％から３７％、当たりが出る確率は１から出ない確率を引いて、６３％から６４％くらいだと考えれば良いことになります。

　　ネイピア数eについての説明

　ネイピア数eについてもう少し詳しく説明します。
　ここでは少し数学の記号を使います。
　まず、『当たる確率』をｎ分の１とします。　　　　　　　　　　　　　　 ⇒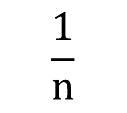    
　次に、『外れる確率』を１から『当たる確率』を引いた数とします。 ⇒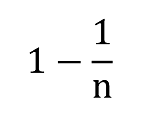 
　最後に、『ｎ回引いた時に当たりが出ない確率』を、
　『外れる確率』をｎ回かけ合わせた数とします　　　　　　　　　　 ⇒ ※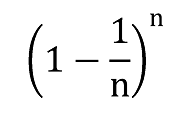
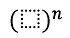　 　※ はｎ回かけ合わせるの意味、数学ではｎ乗と呼びます。
　この時の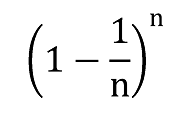のｎがとても大きい数の時（当たりにくいガチャをたくさん回す時）
　の当たりが出ない確率の上限がe分の１となり、大体３７％になります。
　ちなみに、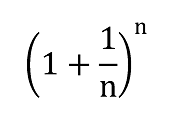はeになります。こちらは大体2.7です。
                    　　　　                  

　当たり確率１％のガチャを１００回回した時の当たりが出ない確率は３７％くらいとわかりました。
　では、このガチャを２００回回した時に当たりが出ない確率はどれだけでしょうか。こちらは１００回の時の確率がわかっていれば簡単です。つまり当たりが出ない確率が３７％のガチャを２回回したと考えれば良いのです。この確率は３７％を２回かけ合わせて大体１３．５％、７から８分の１といったところです。意外と高いのではないでしょうか。
　３００回回した場合は３７％を３回かけ合わせればよいので、ほぼ５％、２０分の１となります。３００回回しても当たらないなんて異常なほど運の悪い人に思えますが、周りに１人くらいいてもおかしくはありませんね。

　ネイピア数eを用いた計算は統計学でもとてもよく使います。
　数式でこの数を見かけたときに、「これはガチャを回す時の確率の数だ。」と思ってみれば、少し親しみが湧いてくるのではないでしょうか。

　三重県の統計情報は「みえDataBox」でご覧いただけます。

   次回のHello！とうけい♪vol.289は、令和７年7月23日（水曜日）掲載予定です。
　お楽しみに！