【Hello!とうけい】vol.95 平均値は"真ん中"とは限らない。？！

　データの特徴を要約する方法の一つが代表値です。
　代表値には、次のものを挙げることができます。

　1.平均値　：　データの全てを足して、データの総数で割った値（データの重心）
　2.中央値　：　データを大きさの順に並べたとき、ちょうど中央の位置にくる値
　3.最頻値　：　度数分布の中で最も多い度数を示す階級に対する値（偶数個の場合は、中央の２つの値の平均値）
　これらのうち、最も一般的なものとして用いられているのが平均値です。

　集団の分布が、図１のような正規分布（左右対称の釣り鐘型をした分布の形）に近い場合には、平均値、中央値、最頻値ともほぼ同じ値を示すことになります。

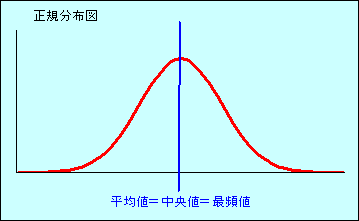
図１

　しかし、平均値には次のような欠点もあります。
　その一つは、特異な数値（外れ値）の影響をうけやすいということです。

　例えば、総務省統計局が公表した平成18年の家計調査（二人以上の世帯）によると１世帯あたりの平均貯蓄現在高は、1,722万円となっています。
　その分布の状況は、図２のようになります。

貯蓄現在高階級別世帯分布（二人以上の世帯）

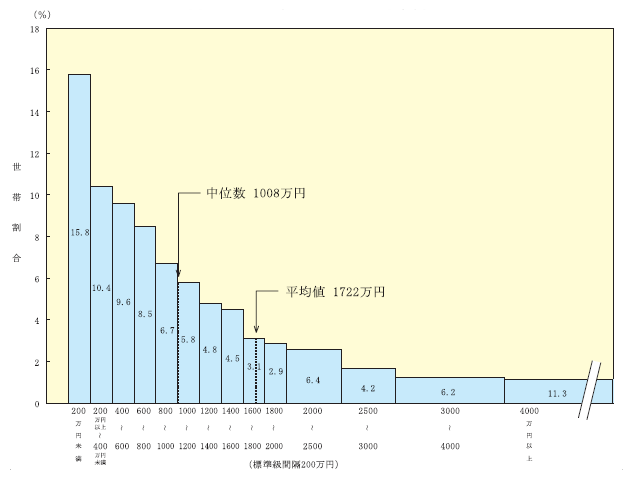
図２

　この分布図をみると、平均値は1,722万円ですが、中央値は1,008万円、最頻値は200万円未満の階級であるということができ、代表値（平均値、中央値、最頻値）に大きな乖離が生じています。
　平均値が、1,722万円と最も高い値を示しているのは、特異値（この例では、一部の人の極端に大きい貯蓄現在高）に大きく影響を受け、平均値を押し上げているためです。このため、約３分の２の世帯が平均値を下回る結果となっています。
　このような場合には、平均値は必ずしもよい代表値とは言えなくなるため、他の代表値（中央値、最頻値）も同時に明記したほうが良いでしょう。
　また、もう一つの欠点としては、図３のようにデータが分布範囲の両端に多く存在している場合には、平均値はデータがあまり存在しないところになってしまいます。

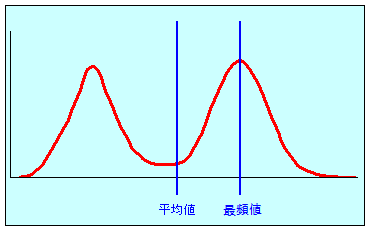
図３

　平均値という言葉には、“真ん中"というイメージがありますが、データを半分半分に分けているという意味ではないことを認識する必要があります。

　三重県の統計情報は「みえDataBox」http://www.pref.mie.jp/DATABOX/に満載です。

　次回のHello!とうけい♪vol.96は、9月12日（水曜日）掲載予定です。お楽しみに！